长沙县星沙中学 郭鹏飞
摘要: 我们习以为常的“良好”设计,在课堂真正实施时发现效果并不尽然,显然是脱离了学情和专业的设计即有“缺陷”与局限性的,我们结合常见几种缺陷设计并提出思考和改进方案。
关键词 设计;缺陷;改进;思考
教学“设计”是为了更好的课堂“生成”,然而有时你觉得是“精心”的,真正在课堂实施时却不起任何思维的“波浪”,其实是大有“原因”的!大家常见“习以为常”的设计是有缺陷及局限性的,结合常见案例谈谈我们的改进与思考:
1.只讲必要性,很少讲充分性(更不用说讲充要性)
案例一:二元一次方程的导入使用“鸡兔同笼”经典问题:鸡兔同笼,上有9头,下有26足,问鸡兔几何?
设计意图 前面经验:使用算术法中的归一法、抬腿法、坐地法等不易想到并且繁琐的事实提出一元一次方程的解法;当下目的:再提出新方法、新模型!
真实课堂 学生的情绪表现是“不屑一顾”,很不来神,和学生交流发现:有简单的一元一次方程就可足矣,何必多此一举即没必要用设两个元的二元一次方程模型!
改进思考 我的例子:联赛每场分出胜负,胜一场记2分,负一场记1分,甲得了16分。①若甲负了4场,则甲胜了几场?②问此轮比赛中,甲胜负几何?
第一小问是铺垫,让“不来神”的学生产生思维定式,以为接下来的第二小问列一元一次方程模型是“万能的”假象!琢磨半天发现“不能“列一元一次方程解答了,必须用新模型“二元一次方程”来了结!
2.只讲纯粹性,很少讲完备性
案例二:如七(下)第四章 相交线与平行线中①“平面内三条直线位置关系”分类其中一种析出“三线八角”;②.还如“箭头型”分类及规律及其拓展!
真实课堂 一般课堂是俗话讲的“萝卜吃一截锴一截”直接出示所要研究的课题图形即静态的呈现问题纯粹图形,至于如何引起与它图形的联系很少点击,所以是断裂的支离破碎的知识节点。
改进思考 我的方法:如①采用剧本的“人物出场法”先任意画出第一条直线,再画第二条直线时引导学生如何画?自然对话出有两种分类:要么与第一条直线相交、要么与第一条直线平行;最后第三条直线“出场”又须分类,前者又有两种情况,即过相交两直线的交点或不过前两条直线的交点;后者也又有两种情况,即与前面两条平行线相交或与前面两条平行线都平行;如此得到“平面内三条直线位置关系”有四种情形,而这正好揭示了整章的图形主题,体现与代数同一现象的分类思想的提醒与觉悟的需要!如②更是如此引导析出七种分类情况,体悟出图形的丰富多彩!也为问题“箭头型”压轴变式题做了“前期铺垫”!
设计意图 与代数的本质接轨(也有分类)、与生活接轨(做事的顺序乃逐一登场而不是“集体冲锋”)、完整性认识本章的核心知识体系即思维导图有图形导图是核心点!更是互动引导体现探究性与合作性让学生一开始学习几何时就有听说读写画算推的基本意识和习惯,让其成为一种学习的“常态”!
3.只讲整体思想,很少讲具体
案例三:如教材26页题目 在一次国际象棋女子挑战赛上,我国女子国际象棋特级大师谢军在苦战15盘后,以净胜俄罗斯棋手加里亚莫娃2分的优异成绩,第三次夺得棋后桂冠,比赛的积分规则是胜了得1分,负得0分,和棋各得0.5分。问两位棋手最后的积分各是多少?(湘教版七年级下册第26页C组第14题)
真实课堂 ⑴常见方法 设谢军和加里亚莫娃的积分分别是x分,y分,则x+y=15,x-y=2,解得x=8.5,y=6.5,即谢军积分是8.5分、加里亚莫娃积分是6.5分; ⑵假设法 因“净胜俄罗斯棋手加里亚莫娃2分”且“比赛的积分规则是胜了得1分”,故可“假设”谢军净胜了2盘,不计负的盘数,于是其余15-2=13盘是“和棋”,从而有谢军得分为2+13÷2=8.5分,加里亚莫娃积分是13÷2=6.5分;整体思考甚是“热闹”,走下讲台课堂交流真实的情况是:学生似懂非懂!
改进思考 我的方法:⑶明白法 设谢军胜a盘、和b盘、负c盘,积分为a×1+b×0.5+c×0=a+1/2b①
则对应的加里亚莫娃负盘、和盘、胜盘,积分为
a×0+b×0.5+c×1=1/2b+c②
无论怎样的结果盘数都满足关系a+b+c=15③,
又“净胜俄罗斯棋手加里亚莫娃2分”故由①-②:
(a+1/2b)-(1/2b+c)=2,即a-c=2④
于是可由③与④联合{ a+b+c=15,a-c=2得出结果,即
③+④ 2a+b=17 ; a+1/2b=8.5分即谢军最后的积分即结合①把前一个等式利用等式的基本性质两边同时除以2得到的!
③-④ b+2c=13,1/2b+c=6.5 分即加里亚莫娃最后的积分即结合②把前一个等式利用等式的基本性质两边同时除以2得到的!
设计意图 整体思想是大格局的思维,学生不易想到!为了开启学生思维让他们肯动脑筋,关注细节具体用好课本,一题多解,体悟具体到整体的战术示范解析中游荡也可取得好的思维水平和能力!
4.只讲本位,很少讲联系
案例四:如化简、合并、因式分解、关联词“且、或”的理解等数学常态现象的处置。
真实课堂 课堂上老师们“一本正经”的满嘴的“数学术语”即从抽象到抽象,当下很多学生“昏昏欲睡”、不甚了了!
改进思考 我的方法:如轻装上阵如同数学化简;“物以类聚”类似数学合并;“瞻前顾后”乃因式分解分解不彻底的提醒驻足的“良方”;比如结构a2+b2=0涉及“且”联想到英语的“and”、电学的“串联”乃至高中的集合的“交集”;再比如ab=0涉及“或”联想到英语的“or”、电学的“并联”乃至高中的集合的“并集”等等跨学科的引领!交织纵横学科,牵手彼此联系,感受丰富多彩!
设计意图 把抽象的东东具体化、形象化,在语言刺激关联联想与发散思维即普遍联系的哲学观念的体验过程中有兴趣的投入、达到化解难点与易错点的目的,为自己将来以后的学习提供一个比较通俗可行的范式!
5.只讲战略,很少讲战术
案例五 关于阶段性章节复习课
真实课堂 很多数学问题,老师们大谈思路如何如何,让学生提起来蛮以为就是那么的,真正做起来时发现好多岔路根本上是“无所作为”!
改进思考 我的方法:国家教材字体要求启示:既讲整体更讲具体才是真正的关心与关注!具体如七(下)§2.整式的乘法复习课:我从五个方面示范引领学生的学习指导即①易错题(具体全部取材于课本练习题、习题、复习题中的判断正误题);②图形题(具体全部取材于课本正文、练习题、习题、复习题中的图形变换题);③重点关注题(具体全部取材于课本例题、习题、复习题中的B、C组题);④阅读拓展题(具体全部取材于课本C组题);⑤其他补充题(课外基础训练中档以上经典题)
设计意图 首先是重视课本,课本是经典;在初级复习阶段是蓝本、是“榜样”,它更是基础弱生的再次升级的基石和机会,也是好生温故知新、螺旋提升的良策!战术示范很重要;整体观最易“绑架人”,让人不敢多言!道理确实是这样,还好说吗?具体最“折腾人”,但最暖心!揭示:平常喜欢折腾自己的人,将来必定是有“出息”的人的哲学引领!
6.只讲“当下”,很少讲“前生”
案例六 提公因式法的“公因式”到底如何析出?
真实课堂 很多老师都是“灌”出来的,再在大量练习模仿中“摸索”出一些基本技巧!
设计意图 基于当下基本理念“教什么比怎么教更重要”,知识学习既讲“当下”更要讲“前生”方便弄懂知识的来龙去脉,站在已有知识的“肩膀上”去有效学习!
改进思考 我的方法:先由小学最大公约数如15与90的最大公约数的析出:15=3×5,90=32×5×2发现最大公约数是3×5(即相同质因数及它们最低次幂的积构成);发现最大公约数的本质是:“几个给定正整数分解质因数的积后,选取相同质因数及它们最低次幂的积”的科学新认知!由特殊数再到一般代数式,提公因式分解因式法中关键点公因式的析出,由前面铺垫不难类比析出(字母)公因式是把每一项的整式改写为“类似质因数的基本式子”积的形式,发现“相同因式及它们最低次幂的积”构成!自然有最小公倍数(如上是32×5×2即所有质因数及它们相同质因数最高次幂的积构成的本质认识提升)与分式加减法中通分用的最简公分母相关!显示找准生长点可创新提升旧认知!显示是创造性的“发现”学习!
7.只讲“本本”,很少讲“创新”
教材解读是教师的基本功,在当下“汗牛充栋”的解读读物中如何走出“重复”,实现“创新”引领,还是有方法的,结合案例下面提出了三个基本方法。
大家共识:处处留心皆学问;然而面对自己熟悉的教材,老师们大多说:教材解读读物当下已是“汗牛充栋”,把教材里里外外基本翻了个“底朝天”了,还有创新解读的空间“余地”吗?其实上述读物大多是停留在基本“继承”即本义的解读层面,完全还可以继续“引申”创新提高层次;兹结合湘教版说几个可以创新的例子:
7.1从基本概念图形中创新
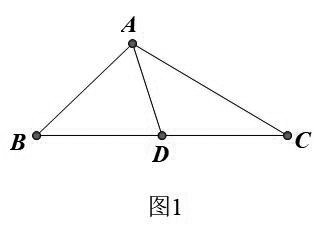
案例七 如三角形重要概念“三角形的中线”,图1D为BC的中点,则称线段AD为△ABC的中线。
真实课堂 仅仅停留在概念的基本描述上。
设计意图 继续“引申”创新提高理解的层次。
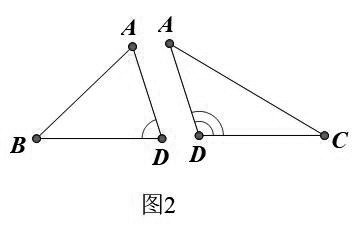
改进思考 我的方法:引申一下 中线AD把△ABC分成两个小三角形即△ABD与△ACD,不难发现:AD=AD、BD=DC、∠ADB与∠ADC互补,而且△ABD与△ACD面积相等,理由很简单:等底同高!
现在把△ABD与△ACD“分离”析出成两个“独立”三角形,图2于是有结论:
两边相等且夹角互补的两个三角形面积相等
如何简单初等的证明?回到图1即可!这个小小的创新证明源于基本概念图的“复位”!完全可以避免用“1/2absina=1/2absin(1800-a),其中两边、的夹角为a和(1800-a)”,后继知识“sina=sin(1800-a)”初中已经删除上移高中了!说明我们的从基本概念图形中创新理解既基础又在学生知识的最近发展区,值得发散效仿!
7.2从基本公式证明一般化中创新
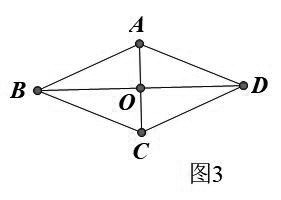
案例八 如菱形的面积公式,图3菱形ABCD的对角线相交于点O,则菱形的面积等于1/2AC×BD。
真实课堂 仅仅停留在课本如下“特殊”证明:
S菱形=4S△ABO=4×1/2AO×BO=1/2(2AO)×(2BO)=1/2AC×BD.显然除了用到“菱形的对角线互相垂直”外,还用到了“菱形的对角线互相平分”这个特殊结论!
设计意图 继续“引申”创新提高理解到更普适的层次。
改进思考 我的方法:引申一下 如果不用后者一般证明:
S菱形=S△ABO+S△BCO+S△CDO+S△DAO
=1/2AO×BO+1/2CO×BO+1/2CO×DO+1/2AO×DO
=1/2BO×(AO+CO)+1/2DO×(AO+CO)
=1/2(OA+CO)×(BO+DO)=1/2AC×BD
不难发现:只用到“对角线互相垂直”这个条件,于是从这个一般证明的过程中发现一般结论:
对角线互相垂直的四边形的面积等于两对角线乘积的一半。
在课堂中自然落地,无需课外“培优”,竞赛中常用到的结论自然析出!
7.3从结构特征追问中创新
案例九 如科学计数法,a×10n(1≤|a|<10,n为整数)在这个特征结构中指数n的本质意义是什么?
真实课堂 几乎从未提到过这个“问题”。
设计意图 对这个“创新”问题老师们怎么看?在你的课堂中“闪现”过吗?看透本质,直接走过去,让学生“亲切”的感受到创新的魅力!
改进思考 我的方法:我们可以如下追问:我们知道科学计数法在湘教版七年级学习正整数指数幂的时候学习到,再到湘教版八年级时学习负整数指数幂的时候再次学习到,所以老师们必须整体单元设计让初次学习的思维方法对后继学习有“正迁移”功能!于是初次在七年级学习科学计数法时我们的设计是:充分利用学生最近知识发展区等最本质的方法(小数点移动规律和乘方的意义)去引导和生成!
回到主题 老师们不妨提示:当一个问题不好处理时“回到”定义或“起始点”不难发现;其次用“像寻原像”的观点或“思路可逆”原理引导,具体仍是特例理解法:
比如已知1.2345×104求原数?仍然是借助“小数点移动规律”逆向溯源即1.2345×104=12.345×104×(1/10)=12.345×(103)[追问括号里的算理,下同]
=12.345×(104)×(1/10)=123.45×(102)=123.45×103×(1/10)=1234.5×10=12345×10×(1/10)=12345
此时自然提出:1.2345×104=12345即是把科学计数法表示数1.2345×104的原数找出了,其实就是把1.2345×104中的1.2345小数点向右移动了四次得到原数12345的!其中指数“4”(即正数+4)符号“+”表示小数点移动的方向是“右”、数值4表示小数点移动的次数是“四”之本质意义;
于是八年级由科学计数法求原数再次学习时,学生在老师的引导回忆下必会自然有下面的等值变形:
比如已知1.2345×10-3求原数?仍然是借助“小数点移动规律”逆向溯源:1.2345×10-3=0.12345×10-3×(10)=0.12345×(10-2)[追问括号里的算理,下同]=0.012345×10-2×(10)=0.012345×(10-1)=
0.0012345×10-1×(10)=(0.0012345)
此时自然提出:1.2345×10-3=0.0012345即是把科学计数法表示数1.2345×10-3的原数找出了,其实就是把1.2345×10-3中的1.2345小数点向左移动了三次得到原数0.0012345的!其中指数“-3”符号“-”表示小数点移动的方向是“左”、数值3表示小数点移动的次数是“三”之本质意义。
最后一般揭示科学计数法a×10n(1≤|a|<10,n为整数)中指数n的本质意义:
当指数n是正数时,符号“+”表示a小数点移动的方向是“右”、数值n表示小数点移动的次数是“n”后得到科学计数法表示数之原数的本质意义;
当指数n是负数时,符号“-”表示a小数点移动的方向是“左”、数值|n|表示小数点移动的次数是“|n|”后得到科学计数法表示数之原数的本质意义!
这个“常见”但不显眼的问题是基于“结构特征”的追问在教材解读中创新提出的,这个思路很重要,因为数学题目的三个主要特征“数值特征、结构关系、图像信息”的发现是创新解题的主要突破口,于是课堂的平时积累解读引领就变得珍贵了;当然还有很多其他“创新”解读的方法,让我们共同努力一起去发掘吧!
当然还有很多课堂设计常见的“病灶”,需要我们左右权衡结合学情尝试设计与课堂调整,方能教学相长有效落地!