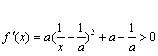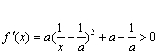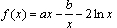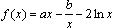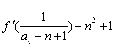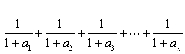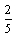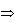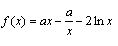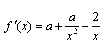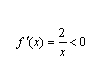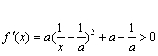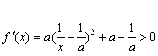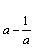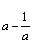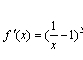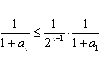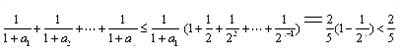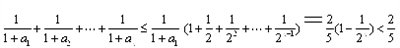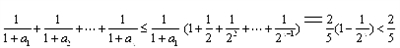长沙市一中数学高级教师 蒋楚辉

【知识范畴】函数、导数、数列、不等式综合问题

例:已知函数 ，

，f (1)=0.

（1）若函数f (x)在其定义域内为单调函数，求a的取值范围.

（2）若函数f (x)的图象在x = 1处的切线的斜率为0，且

an+1 = ，已知a1 = 4，求证an≥2n + 2.

（3）在（2）的条件下，试比较

与 的大小，并说明理由。

【思路分析】第（1）问实为“超越函数”的单调性问题，求解策略是将“函数f (x)在区间A上单调”等价于“x∈A时f′(x)≥0（f′(x)≤0）恒成立”；第（2）问有关通项an的不等式证明，思维的切入方法可以从求得通项公式后进行证明，也可考察通项的前n项，总结规律，然后用数学归纳法证明，还可以通过构造函数，利用导数进行证明；（3）有关数列前n项和的不等式关系探究，常用方法有适当放缩通项，将其放缩后化归为可求和的特殊数列的通项，求和后再适当放缩最终实现问题求解。

【解析】（1）f (1) = a-b = 0 a = b，则 .

∴ ，要使f (x)在定义域(0, +∞)内为单调函数，

则在[0，+∞)内，f′(x)恒大于0或恒小于0.

当a = 0时，

在(0, +∞)内恒成立.

当a＞0时，要使

恒成立，则 ＞0，解得a＞1.

当a＜0时，要使

＜0恒成立，则 ＜0，解得a＜-1.

故a的取值范围为a＞1或a＜-1或a = 0.

（2）由已知f ′(1)=0，即a +a-2=0得a=1，

∴ ，

∴an+1 =(an-n)2-n2 =1= an2 -2nan+1.

由数学归纳法：

当n=1时，a1=4≥2×1+ 2，不等式成立.

假设n=k时，不等式an≥2k+2成立，即ak-2k≥2也成立.

则当n=k+1时，ak+1=ak (ak -2k)+1≥(2k+2)×2+1=4k+5＞2 (k+1)+2成立.

故对一切n∈N*都有an≥2n + 2成立.

（3）由（2）得an=an-1(an-1- 2n+2)+1≥an-1[2(n-1)+2-2n+ 2]+1=2an-1+1. 于是an+1≥2(an-1 +1)(n≥2).

所以a2+1≥2(a1+1)，a3+1≥2(a2 +1)…

an+1≥2(an-1+1)，累乘得an +1≥2n-1(a1+1)，

则 (n≥2).

所以=

【命题立意】函数、导数、不等式、数列的综合问题是高考命题的热点，常以压轴题形式出现，主要考查学生的思维能力；掌握基本题型及解法是基础，依据题设情境，灵活应用转化化归思想、数形结合思想、函数与方程思想，将问题化归为基本问题求解是关键，同时必须努力提高分析能力、创新意识，讲究思维的灵活性和深刻性。